6 º ano
NÚMEROS E OPERAÇÕES, GRANDEZAS E MEDIDAS
Conteúdo: multiplicações, medidas de superfície, unidades de área, formas geométricas, quadrados perfeitos ou números quadrados, potências e ângulos.
JUSTIFICATIVA
Encaminhar para o aluno resolver problemas do seu
cotidiano relacionados à unidades de medidas, partindo de situações simples.
Objetivos:
- Construir os conceitos básicos da tabuada de multiplicar e suas regularidades e padrões entre si;
- Relacionar tabuada com medidas de área, sejam capazes de construir diferentes figuras com mesma áreas;
- Reconhecer as diferentes formas de calcular a área de quadrados e retângulos;
- Utilizar as unidades padrões de superfícies, bem como seus múltiplos e submúltiplos;
- Analisar múltiplos e divisores de números naturais;
- Deduzir as fórmulas de cálculo de aérea e perímetro de figuras geométricas;
- Deduzir maneiras de como calcular de área s através de enquadramentos e decomposição de figuras.
ATIVIDADE I: Construindo a tabuada na forma de quadrados:
Materiais: 1 folha A3 com quadriculada de 1cm2, por grupo,
lápis de cor e régua.
1: Traçado dos quadrados em diagonal
1.1. Desenhar na folha quadriculada um quadrado de lado
um, começando num ponto qualquer na zona superior esquerda da folha e deixando
uma pequena margem.
1.2. Unindo o vértice inferior direito do
primeiro quadrado com o vértice superior esquerdo do segundo quadrado e assim
sucessivamente, desenhar quadrados de lados 2, 3, 4, 5 e 6.
1.3. Pintar o interior de todos os quadrados, usando
sempre a mesma cor.
2: Traçando retângulos:

2.1 . Traçar retas prolongando-se os lados dos quadrados já desenhados.
2.2.Pintar, da mesma cor, as figuras geometricamente iguais resultantes do traçado feito.
 2.3. No interior de cada figura desenhada, registar o valor da respectiva área, sob a forma
2.3. No interior de cada figura desenhada, registar o valor da respectiva área, sob a forma
de uma multiplicação, em que os fatores são o número de linhas e o número de
quadrículas por linha. Ex.: A área de um retângulo com 6 quadradinho pode resultar de
1x6 ou 2x3, consoante(ao lado do outro) o retângulo ocupe 1 linha com 6 quadrículas, ou 2 linhas com 3 quadradinho de cada uma.
3: Continue o traçando:
A construção que acabou de fazer pode ser continuada. Continue-a, seguindo os
procedimentos anteriores, até que a folha de papel o permita.
Parte II: Procurando regularidades na tabuada e nas formas.
Observe a construção feita. Descubra e registe regularidades.
Parte III: Explorando a tabuada e suas formas
Questões orientadoras
1. Procurar todas as figuras de área 12. Quantas figuras se encontram? Identificar as figuras geometricamente iguais. Quantos grupos diferentes se encontram? Que representam s diferentes factores de 12?
2. Indicar se é verdadeira ou falsa a afirmação: “Duas figuras geometricamente iguais são equivalentes, mas duas figuras equivalentes podem não ser geometricamente iguais”. Justificar a resposta.
3. Dar exemplos de figuras equivalentes mas que não sejam geometricamente iguais. Localizar todas as figuras de perímetro 20. Qual destas figuras tem maior área? Acontecerá o mesmo para outras figuras isoparamétricas(figuras de perímetros iguais)? m que regularidades se encontram?
4. Localizar os múltiplos de 2, de 3, de 4, de 5, de 6, .... Onde estão, na tabuada e suas formas os múltiplos comuns a 2 e a 4? Porquê? E os múltiplos comuns a 2 e a 3? Porquê?
5. Procurar todas as figuras de área 12 e de área 15. Usar as decomposições do 12 e do 15 em fatores para calcular 12 x 15. Alguma(s) combinação de fatores tornou o cálculo mais simples? Qual/Quais? Porquê?
6. Calcular agora a área do retângulo representada por 12 x 15 de uma outra forma. Haverá alguma forma de representar a área deste retângulo através de retângulos representados na tabuada? Se sim, que retângulos são estes?
7. A sala da Joana tem de área 25 m2 e suas formas” para descobrir que diferentes formas geométricas pode ter a sala da Maria. Desenhar um esquema da sala em papel quadriculado.
8. Na “tabuada geométrica” há figuras cuja área se pode representar sob a forma de, um
produto de dois fatores iguais. Que figuras são? Como descrever a sua localização?
Representar a sua área sob a forma de potência.
9. O que representam geometricamente as potências de expoente 2? Qual é o número quadrado que vem a seguir ao 64? E a seguir? E a seguir?...
O numero 40 é um quadrado perfeito? Porquê?
Escolher duas figuras geometricamente iguais e localizá-las na “tabuada geométrica”. As áreas destas figuras podem representar-se sob a forma de potência de expoente 2?
10. Os quadrados são retângulos porque têm os ângulos retos.
Indicar se é verdadeira ou falsa a afirmação: “Os quadrados são retângulos mas nem todos os retângulos são quadrados”. Justificar a resposta.
11. Há números na “tabuada geométrica” a que só pode associar-se um par de figuras geometricamente iguais. Que números são esses?
Fonte:
Escola Superior de Educação do Instituto Politécnico de Setúbal Programa de Formação Contínua em Matemática para Professores dos 1.º e 2.º Ciclos do Ensino Básico: 2010 ‐ 2011
. PARTE IV - ATIVIDADES GERAIS
PERÍMETRO DE UM POLÍGONO

O perímetro de uma figura plana fechada é o comprimento da linha que limita a figura.
É o comprimento da linha que limita o polígono ou a soma das medidas dos seus lados.

.
Perímetro=100+50+97+10+13+10+10+30= 320m
PERÍMETRO DE UM POLÍGONO:
Retângulo

Quadrado
P = l + l + l+ l
Perímetro = 4 x l
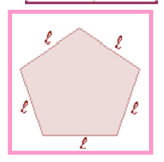
Pentágono
P= l + l + l + l + l
Perímetro= 5 x l
DETERMINAÇÃO NA PRÁTICA
Diâmetro – Corda que passa pelo centro da circunferência.(AC)
 Diâmetro (d)=2xraio(r)
Diâmetro (d)=2xraio(r)
Raio – Metade do diâmetro.(AO , OC, OB)
Círculo é uma figura geométrica plana constituída por uma circunferência e pelo conjunto de pontos do seu espaço interior
DETERMINAÇÃO PRÁTICA DO π
O quociente do comprimento de uma circunferência pelo seu diâmetro tem sempre o mesmo valor que se designa por π (PI). O seu valor, aproximado às centésimas, é de 3,14.
PERÍMETRO DO CÍRCULO OU COMPRIMENTO DA CIRCUNFERÊNCIA
 Perímetro de um círculo é o comprimento da circunferência que o limita.
Perímetro de um círculo é o comprimento da circunferência que o limita.
Para calcularmos o perímetro do círculo multiplicamos π pelo comprimento do diâmetro.
P = π X d
Como diâmetro = 2x raio podemos também dizer que:
PERÍMETRO DO CÍRCULO (comprimento da circunferência) = 2 x π x raio
MEDIDAS DE COMPRIMENTO (METRO)
A unidade fundamental de medidas de comprimento é o metro, indicado por m.
FIGURAS EQUIVALENTES

Duas figuras são congruentes se sobrepuserem ponto por ponto.
Figuras equivalentes são aquelas que têm a mesma área.
 Figuras planas congruentes são sempre equivalentes.
Figuras planas congruentes são sempre equivalentes.
Figuras planas equivalentes têm sempre a mesma área, mas podem ser, ou não, congruentes.
Figuras geometricamente iguais
ÁREAS EQUIVALENTES
Duas superfícies são equivalentes quando têm a mesma área, como por exemplo, as superfícies A e B.
A medida de área de uma superfície é igual ao número de vezes que a unidade de área escolhida cabe na superfície considerada.
UNIDADE DE ÁREA DO SISTEMA MÉTRICO
 Esta figura é formada por quatro quadrados.
Esta figura é formada por quatro quadrados.
Como a área de cada quadrado é 1 , a área
desta figura é 4 ,

2.1 . Traçar retas prolongando-se os lados dos quadrados já desenhados.
2.2.Pintar, da mesma cor, as figuras geometricamente iguais resultantes do traçado feito.
 2.3. No interior de cada figura desenhada, registar o valor da respectiva área, sob a forma
2.3. No interior de cada figura desenhada, registar o valor da respectiva área, sob a formade uma multiplicação, em que os fatores são o número de linhas e o número de
quadrículas por linha. Ex.: A área de um retângulo com 6 quadradinho pode resultar de
1x6 ou 2x3, consoante(ao lado do outro) o retângulo ocupe 1 linha com 6 quadrículas, ou 2 linhas com 3 quadradinho de cada uma.
A construção que acabou de fazer pode ser continuada. Continue-a, seguindo os
procedimentos anteriores, até que a folha de papel o permita.
Parte II: Procurando regularidades na tabuada e nas formas.
Observe a construção feita. Descubra e registe regularidades.
Parte III: Explorando a tabuada e suas formas
Questões orientadoras
1. Procurar todas as figuras de área 12. Quantas figuras se encontram? Identificar as figuras geometricamente iguais. Quantos grupos diferentes se encontram? Que representam s diferentes factores de 12?
2. Indicar se é verdadeira ou falsa a afirmação: “Duas figuras geometricamente iguais são equivalentes, mas duas figuras equivalentes podem não ser geometricamente iguais”. Justificar a resposta.
3. Dar exemplos de figuras equivalentes mas que não sejam geometricamente iguais. Localizar todas as figuras de perímetro 20. Qual destas figuras tem maior área? Acontecerá o mesmo para outras figuras isoparamétricas(figuras de perímetros iguais)? m que regularidades se encontram?
4. Localizar os múltiplos de 2, de 3, de 4, de 5, de 6, .... Onde estão, na tabuada e suas formas os múltiplos comuns a 2 e a 4? Porquê? E os múltiplos comuns a 2 e a 3? Porquê?
5. Procurar todas as figuras de área 12 e de área 15. Usar as decomposições do 12 e do 15 em fatores para calcular 12 x 15. Alguma(s) combinação de fatores tornou o cálculo mais simples? Qual/Quais? Porquê?
6. Calcular agora a área do retângulo representada por 12 x 15 de uma outra forma. Haverá alguma forma de representar a área deste retângulo através de retângulos representados na tabuada? Se sim, que retângulos são estes?
7. A sala da Joana tem de área 25 m2 e suas formas” para descobrir que diferentes formas geométricas pode ter a sala da Maria. Desenhar um esquema da sala em papel quadriculado.
8. Na “tabuada geométrica” há figuras cuja área se pode representar sob a forma de, um
produto de dois fatores iguais. Que figuras são? Como descrever a sua localização?
Representar a sua área sob a forma de potência.
9. O que representam geometricamente as potências de expoente 2? Qual é o número quadrado que vem a seguir ao 64? E a seguir? E a seguir?...
O numero 40 é um quadrado perfeito? Porquê?
Escolher duas figuras geometricamente iguais e localizá-las na “tabuada geométrica”. As áreas destas figuras podem representar-se sob a forma de potência de expoente 2?
10. Os quadrados são retângulos porque têm os ângulos retos.
Indicar se é verdadeira ou falsa a afirmação: “Os quadrados são retângulos mas nem todos os retângulos são quadrados”. Justificar a resposta.
11. Há números na “tabuada geométrica” a que só pode associar-se um par de figuras geometricamente iguais. Que números são esses?
Fonte:
Escola Superior de Educação do Instituto Politécnico de Setúbal Programa de Formação Contínua em Matemática para Professores dos 1.º e 2.º Ciclos do Ensino Básico: 2010 ‐ 2011
. PARTE IV - ATIVIDADES GERAIS
PERÍMETRO DE UM POLÍGONO

O perímetro de uma figura plana fechada é o comprimento da linha que limita a figura.
É o comprimento da linha que limita o polígono ou a soma das medidas dos seus lados.

.
Perímetro=100+50+97+10+13+10+10+30= 320m
PERÍMETRO DE UM POLÍGONO:
Exemplos
b - base ou comprimento
h - altura ou largura
Perímetro = 2b + 2h,onde b= base h=altura

Quadrado
P = l + l + l+ l
Perímetro = 4 x l

Pentágono
P= l + l + l + l + l
Perímetro= 5 x l
V - ELEMENTOS DE UMA CIRCUNFERÊNCIA
Diâmetro – Corda que passa pelo centro da circunferência.(AC)
 Diâmetro (d)=2xraio(r)
Diâmetro (d)=2xraio(r)Raio – Metade do diâmetro.(AO , OC, OB)
Círculo é uma figura geométrica plana constituída por uma circunferência e pelo conjunto de pontos do seu espaço interior
DETERMINAÇÃO PRÁTICA DO π
O quociente do comprimento de uma circunferência pelo seu diâmetro tem sempre o mesmo valor que se designa por π (PI). O seu valor, aproximado às centésimas, é de 3,14.
PERÍMETRO DO CÍRCULO OU COMPRIMENTO DA CIRCUNFERÊNCIA
 Perímetro de um círculo é o comprimento da circunferência que o limita.
Perímetro de um círculo é o comprimento da circunferência que o limita.Para calcularmos o perímetro do círculo multiplicamos π pelo comprimento do diâmetro.
P = π X d
Como diâmetro = 2x raio podemos também dizer que:
PERÍMETRO DO CÍRCULO (comprimento da circunferência) = 2 x π x raio
MEDIDAS DE COMPRIMENTO (METRO)
A unidade fundamental de medidas de comprimento é o metro, indicado por m.
FIGURAS EQUIVALENTES

Duas figuras são congruentes se sobrepuserem ponto por ponto.
Figuras equivalentes são aquelas que têm a mesma área.
 Figuras planas congruentes são sempre equivalentes.
Figuras planas congruentes são sempre equivalentes.Figuras planas equivalentes têm sempre a mesma área, mas podem ser, ou não, congruentes.
Figuras geometricamente iguais
ÁREAS EQUIVALENTES
Duas superfícies são equivalentes quando têm a mesma área, como por exemplo, as superfícies A e B.
A medida de área de uma superfície é igual ao número de vezes que a unidade de área escolhida cabe na superfície considerada.
A medida da área depende dependa da unida escolhida.
UNIDADE DE ÁREA DO SISTEMA MÉTRICO
O metro quadrado representa a área de um quadrado de 1 metro de lado e é a unidade de área do sistema métrico.
RECORDA
 Esta figura é formada por quatro quadrados.
Esta figura é formada por quatro quadrados.Como a área de cada quadrado é 1 , a área
desta figura é 4 ,
1 m2
= 100 dm2 5 cm2 = 0,05 dm2
ÁREA DO TRIÂNGULO
Área do triângulo= b x h
2
b = base
h = altura
ÁREA DO CÍRCULO
Área= π .r2
r2 =
r x r
r = raio
raio = diâmetro
2
ÁREA DO RETÂNGULO E DO QUADRADO
Área do retângulo = b x a
b= base ; a= altura
ÁREA DO PARALELOGRAMO
Área do paralelogramo = b x a
b= base ; a= altura
ÁREAS POR DECOMPOSIÇÃO

ÁREA POR ENQUADRAMENTO

Nem sempre é possível determinar o valor exato da medida da área de uma superfície. Nestes casos, procuramos um valor aproximado, enquadrando a superfície.
A medida da área da piscina é maior que 33 m2.
A medida da
área da piscina é menor que 53 m2.
33 m2
< área da piscina < 53 m2
Pode-se explorar de diferentes maneiras as fórmulas de cálculos de área e perímetros das figuras geométricas.



























