”Para os matemáticos, um eterno problema é explicar ao grande público que a importância da Matemática vai além de sua aplicabilidade. É como explicar a alguém que nunca ouviu música e beleza de uma melodia… Que se aprenda a Matemática que se resolvem problemas práticos da vida, mas que não se pense que esta é a sua qualidade essencial. Existe uma grande tradição cultural a ser preservada e enriquecida, em cada geração." Chandier & Edwards Mathematical Intelligencer. p.35, 1998.
Mostrando postagens com marcador matemática.. Mostrar todas as postagens
Mostrando postagens com marcador matemática.. Mostrar todas as postagens
quarta-feira, 17 de maio de 2017
segunda-feira, 22 de agosto de 2016
TABUADA, MEDIDAS E OPERAÇÕES
6 º ano
NÚMEROS E OPERAÇÕES, GRANDEZAS E MEDIDAS
Conteúdo: multiplicações, medidas de superfície, unidades de área, formas geométricas, quadrados perfeitos ou números quadrados, potências e ângulos.
JUSTIFICATIVA
Encaminhar para o aluno resolver problemas do seu
cotidiano relacionados à unidades de medidas, partindo de situações simples.
Objetivos:
- Construir os conceitos básicos da tabuada de multiplicar e suas regularidades e padrões entre si;
- Relacionar tabuada com medidas de área, sejam capazes de construir diferentes figuras com mesma áreas;
- Reconhecer as diferentes formas de calcular a área de quadrados e retângulos;
- Utilizar as unidades padrões de superfícies, bem como seus múltiplos e submúltiplos;
- Analisar múltiplos e divisores de números naturais;
- Deduzir as fórmulas de cálculo de aérea e perímetro de figuras geométricas;
- Deduzir maneiras de como calcular de área s através de enquadramentos e decomposição de figuras.
ATIVIDADE I: Construindo a tabuada na forma de quadrados:
Materiais: 1 folha A3 com quadriculada de 1cm2, por grupo,
lápis de cor e régua.
1: Traçado dos quadrados em diagonal
1.1. Desenhar na folha quadriculada um quadrado de lado
um, começando num ponto qualquer na zona superior esquerda da folha e deixando
uma pequena margem.
1.2. Unindo o vértice inferior direito do
primeiro quadrado com o vértice superior esquerdo do segundo quadrado e assim
sucessivamente, desenhar quadrados de lados 2, 3, 4, 5 e 6.
1.3. Pintar o interior de todos os quadrados, usando
sempre a mesma cor.
2: Traçando retângulos:

2.1 . Traçar retas prolongando-se os lados dos quadrados já desenhados.
2.2.Pintar, da mesma cor, as figuras geometricamente iguais resultantes do traçado feito.
 2.3. No interior de cada figura desenhada, registar o valor da respectiva área, sob a forma
2.3. No interior de cada figura desenhada, registar o valor da respectiva área, sob a forma
de uma multiplicação, em que os fatores são o número de linhas e o número de
quadrículas por linha. Ex.: A área de um retângulo com 6 quadradinho pode resultar de
1x6 ou 2x3, consoante(ao lado do outro) o retângulo ocupe 1 linha com 6 quadrículas, ou 2 linhas com 3 quadradinho de cada uma.
3: Continue o traçando:
A construção que acabou de fazer pode ser continuada. Continue-a, seguindo os
procedimentos anteriores, até que a folha de papel o permita.
Parte II: Procurando regularidades na tabuada e nas formas.
Observe a construção feita. Descubra e registe regularidades.
Parte III: Explorando a tabuada e suas formas
Questões orientadoras
1. Procurar todas as figuras de área 12. Quantas figuras se encontram? Identificar as figuras geometricamente iguais. Quantos grupos diferentes se encontram? Que representam s diferentes factores de 12?
2. Indicar se é verdadeira ou falsa a afirmação: “Duas figuras geometricamente iguais são equivalentes, mas duas figuras equivalentes podem não ser geometricamente iguais”. Justificar a resposta.
3. Dar exemplos de figuras equivalentes mas que não sejam geometricamente iguais. Localizar todas as figuras de perímetro 20. Qual destas figuras tem maior área? Acontecerá o mesmo para outras figuras isoparamétricas(figuras de perímetros iguais)? m que regularidades se encontram?
4. Localizar os múltiplos de 2, de 3, de 4, de 5, de 6, .... Onde estão, na tabuada e suas formas os múltiplos comuns a 2 e a 4? Porquê? E os múltiplos comuns a 2 e a 3? Porquê?
5. Procurar todas as figuras de área 12 e de área 15. Usar as decomposições do 12 e do 15 em fatores para calcular 12 x 15. Alguma(s) combinação de fatores tornou o cálculo mais simples? Qual/Quais? Porquê?
6. Calcular agora a área do retângulo representada por 12 x 15 de uma outra forma. Haverá alguma forma de representar a área deste retângulo através de retângulos representados na tabuada? Se sim, que retângulos são estes?
7. A sala da Joana tem de área 25 m2 e suas formas” para descobrir que diferentes formas geométricas pode ter a sala da Maria. Desenhar um esquema da sala em papel quadriculado.
8. Na “tabuada geométrica” há figuras cuja área se pode representar sob a forma de, um
produto de dois fatores iguais. Que figuras são? Como descrever a sua localização?
Representar a sua área sob a forma de potência.
9. O que representam geometricamente as potências de expoente 2? Qual é o número quadrado que vem a seguir ao 64? E a seguir? E a seguir?...
O numero 40 é um quadrado perfeito? Porquê?
Escolher duas figuras geometricamente iguais e localizá-las na “tabuada geométrica”. As áreas destas figuras podem representar-se sob a forma de potência de expoente 2?
10. Os quadrados são retângulos porque têm os ângulos retos.
Indicar se é verdadeira ou falsa a afirmação: “Os quadrados são retângulos mas nem todos os retângulos são quadrados”. Justificar a resposta.
11. Há números na “tabuada geométrica” a que só pode associar-se um par de figuras geometricamente iguais. Que números são esses?
Fonte:
Escola Superior de Educação do Instituto Politécnico de Setúbal Programa de Formação Contínua em Matemática para Professores dos 1.º e 2.º Ciclos do Ensino Básico: 2010 ‐ 2011
. PARTE IV - ATIVIDADES GERAIS
PERÍMETRO DE UM POLÍGONO

O perímetro de uma figura plana fechada é o comprimento da linha que limita a figura.
É o comprimento da linha que limita o polígono ou a soma das medidas dos seus lados.

.
Perímetro=100+50+97+10+13+10+10+30= 320m
PERÍMETRO DE UM POLÍGONO:
Retângulo

Quadrado
P = l + l + l+ l
Perímetro = 4 x l
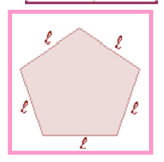
Pentágono
P= l + l + l + l + l
Perímetro= 5 x l
DETERMINAÇÃO NA PRÁTICA
Diâmetro – Corda que passa pelo centro da circunferência.(AC)
 Diâmetro (d)=2xraio(r)
Diâmetro (d)=2xraio(r)
Raio – Metade do diâmetro.(AO , OC, OB)
Círculo é uma figura geométrica plana constituída por uma circunferência e pelo conjunto de pontos do seu espaço interior
DETERMINAÇÃO PRÁTICA DO π
O quociente do comprimento de uma circunferência pelo seu diâmetro tem sempre o mesmo valor que se designa por π (PI). O seu valor, aproximado às centésimas, é de 3,14.
PERÍMETRO DO CÍRCULO OU COMPRIMENTO DA CIRCUNFERÊNCIA
 Perímetro de um círculo é o comprimento da circunferência que o limita.
Perímetro de um círculo é o comprimento da circunferência que o limita.
Para calcularmos o perímetro do círculo multiplicamos π pelo comprimento do diâmetro.
P = π X d
Como diâmetro = 2x raio podemos também dizer que:
PERÍMETRO DO CÍRCULO (comprimento da circunferência) = 2 x π x raio
MEDIDAS DE COMPRIMENTO (METRO)
A unidade fundamental de medidas de comprimento é o metro, indicado por m.
FIGURAS EQUIVALENTES

Duas figuras são congruentes se sobrepuserem ponto por ponto.
Figuras equivalentes são aquelas que têm a mesma área.
 Figuras planas congruentes são sempre equivalentes.
Figuras planas congruentes são sempre equivalentes.
Figuras planas equivalentes têm sempre a mesma área, mas podem ser, ou não, congruentes.
Figuras geometricamente iguais
ÁREAS EQUIVALENTES
Duas superfícies são equivalentes quando têm a mesma área, como por exemplo, as superfícies A e B.
A medida de área de uma superfície é igual ao número de vezes que a unidade de área escolhida cabe na superfície considerada.
UNIDADE DE ÁREA DO SISTEMA MÉTRICO
 Esta figura é formada por quatro quadrados.
Esta figura é formada por quatro quadrados.
Como a área de cada quadrado é 1 , a área
desta figura é 4 ,

2.1 . Traçar retas prolongando-se os lados dos quadrados já desenhados.
2.2.Pintar, da mesma cor, as figuras geometricamente iguais resultantes do traçado feito.
 2.3. No interior de cada figura desenhada, registar o valor da respectiva área, sob a forma
2.3. No interior de cada figura desenhada, registar o valor da respectiva área, sob a formade uma multiplicação, em que os fatores são o número de linhas e o número de
quadrículas por linha. Ex.: A área de um retângulo com 6 quadradinho pode resultar de
1x6 ou 2x3, consoante(ao lado do outro) o retângulo ocupe 1 linha com 6 quadrículas, ou 2 linhas com 3 quadradinho de cada uma.
A construção que acabou de fazer pode ser continuada. Continue-a, seguindo os
procedimentos anteriores, até que a folha de papel o permita.
Parte II: Procurando regularidades na tabuada e nas formas.
Observe a construção feita. Descubra e registe regularidades.
Parte III: Explorando a tabuada e suas formas
Questões orientadoras
1. Procurar todas as figuras de área 12. Quantas figuras se encontram? Identificar as figuras geometricamente iguais. Quantos grupos diferentes se encontram? Que representam s diferentes factores de 12?
2. Indicar se é verdadeira ou falsa a afirmação: “Duas figuras geometricamente iguais são equivalentes, mas duas figuras equivalentes podem não ser geometricamente iguais”. Justificar a resposta.
3. Dar exemplos de figuras equivalentes mas que não sejam geometricamente iguais. Localizar todas as figuras de perímetro 20. Qual destas figuras tem maior área? Acontecerá o mesmo para outras figuras isoparamétricas(figuras de perímetros iguais)? m que regularidades se encontram?
4. Localizar os múltiplos de 2, de 3, de 4, de 5, de 6, .... Onde estão, na tabuada e suas formas os múltiplos comuns a 2 e a 4? Porquê? E os múltiplos comuns a 2 e a 3? Porquê?
5. Procurar todas as figuras de área 12 e de área 15. Usar as decomposições do 12 e do 15 em fatores para calcular 12 x 15. Alguma(s) combinação de fatores tornou o cálculo mais simples? Qual/Quais? Porquê?
6. Calcular agora a área do retângulo representada por 12 x 15 de uma outra forma. Haverá alguma forma de representar a área deste retângulo através de retângulos representados na tabuada? Se sim, que retângulos são estes?
7. A sala da Joana tem de área 25 m2 e suas formas” para descobrir que diferentes formas geométricas pode ter a sala da Maria. Desenhar um esquema da sala em papel quadriculado.
8. Na “tabuada geométrica” há figuras cuja área se pode representar sob a forma de, um
produto de dois fatores iguais. Que figuras são? Como descrever a sua localização?
Representar a sua área sob a forma de potência.
9. O que representam geometricamente as potências de expoente 2? Qual é o número quadrado que vem a seguir ao 64? E a seguir? E a seguir?...
O numero 40 é um quadrado perfeito? Porquê?
Escolher duas figuras geometricamente iguais e localizá-las na “tabuada geométrica”. As áreas destas figuras podem representar-se sob a forma de potência de expoente 2?
10. Os quadrados são retângulos porque têm os ângulos retos.
Indicar se é verdadeira ou falsa a afirmação: “Os quadrados são retângulos mas nem todos os retângulos são quadrados”. Justificar a resposta.
11. Há números na “tabuada geométrica” a que só pode associar-se um par de figuras geometricamente iguais. Que números são esses?
Fonte:
Escola Superior de Educação do Instituto Politécnico de Setúbal Programa de Formação Contínua em Matemática para Professores dos 1.º e 2.º Ciclos do Ensino Básico: 2010 ‐ 2011
. PARTE IV - ATIVIDADES GERAIS
PERÍMETRO DE UM POLÍGONO

O perímetro de uma figura plana fechada é o comprimento da linha que limita a figura.
É o comprimento da linha que limita o polígono ou a soma das medidas dos seus lados.

.
Perímetro=100+50+97+10+13+10+10+30= 320m
PERÍMETRO DE UM POLÍGONO:
Exemplos
b - base ou comprimento
h - altura ou largura
Perímetro = 2b + 2h,onde b= base h=altura

Quadrado
P = l + l + l+ l
Perímetro = 4 x l

Pentágono
P= l + l + l + l + l
Perímetro= 5 x l
V - ELEMENTOS DE UMA CIRCUNFERÊNCIA
Diâmetro – Corda que passa pelo centro da circunferência.(AC)
 Diâmetro (d)=2xraio(r)
Diâmetro (d)=2xraio(r)Raio – Metade do diâmetro.(AO , OC, OB)
Círculo é uma figura geométrica plana constituída por uma circunferência e pelo conjunto de pontos do seu espaço interior
DETERMINAÇÃO PRÁTICA DO π
O quociente do comprimento de uma circunferência pelo seu diâmetro tem sempre o mesmo valor que se designa por π (PI). O seu valor, aproximado às centésimas, é de 3,14.
PERÍMETRO DO CÍRCULO OU COMPRIMENTO DA CIRCUNFERÊNCIA
 Perímetro de um círculo é o comprimento da circunferência que o limita.
Perímetro de um círculo é o comprimento da circunferência que o limita.Para calcularmos o perímetro do círculo multiplicamos π pelo comprimento do diâmetro.
P = π X d
Como diâmetro = 2x raio podemos também dizer que:
PERÍMETRO DO CÍRCULO (comprimento da circunferência) = 2 x π x raio
MEDIDAS DE COMPRIMENTO (METRO)
A unidade fundamental de medidas de comprimento é o metro, indicado por m.
FIGURAS EQUIVALENTES

Duas figuras são congruentes se sobrepuserem ponto por ponto.
Figuras equivalentes são aquelas que têm a mesma área.
 Figuras planas congruentes são sempre equivalentes.
Figuras planas congruentes são sempre equivalentes.Figuras planas equivalentes têm sempre a mesma área, mas podem ser, ou não, congruentes.
Figuras geometricamente iguais
ÁREAS EQUIVALENTES
Duas superfícies são equivalentes quando têm a mesma área, como por exemplo, as superfícies A e B.
A medida de área de uma superfície é igual ao número de vezes que a unidade de área escolhida cabe na superfície considerada.
A medida da área depende dependa da unida escolhida.
UNIDADE DE ÁREA DO SISTEMA MÉTRICO
O metro quadrado representa a área de um quadrado de 1 metro de lado e é a unidade de área do sistema métrico.
RECORDA
 Esta figura é formada por quatro quadrados.
Esta figura é formada por quatro quadrados.Como a área de cada quadrado é 1 , a área
desta figura é 4 ,
1 m2
= 100 dm2 5 cm2 = 0,05 dm2
ÁREA DO TRIÂNGULO
Área do triângulo= b x h
2
b = base
h = altura
ÁREA DO CÍRCULO
Área= π .r2
r2 =
r x r
r = raio
raio = diâmetro
2
ÁREA DO RETÂNGULO E DO QUADRADO
Área do retângulo = b x a
b= base ; a= altura
ÁREA DO PARALELOGRAMO
Área do paralelogramo = b x a
b= base ; a= altura
ÁREAS POR DECOMPOSIÇÃO

ÁREA POR ENQUADRAMENTO

Nem sempre é possível determinar o valor exato da medida da área de uma superfície. Nestes casos, procuramos um valor aproximado, enquadrando a superfície.
A medida da área da piscina é maior que 33 m2.
A medida da
área da piscina é menor que 53 m2.
33 m2
< área da piscina < 53 m2
Pode-se explorar de diferentes maneiras as fórmulas de cálculos de área e perímetros das figuras geométricas.
segunda-feira, 9 de maio de 2016
VAMOS JOGAR UM POUCO?
JOGO DOS PALITOS DE FÓSFOROS!
Eu estava vasculhando meus arquivos da época da FACULDADE olha só que encontrei: o jogo dos palitos, logo abaixo irei postar o link da apostila dos jogos e das repostas e também um simulação online para você jogar, grande abraço Prof. Wendel, veja o texto dele:
"Geralmente não paramos para refletir sobre a grande importância do fósforo na vida das pessoas, pois, no mundo da informatização e dos avanços tecnológico, ainda sim em praticamente todas as casas se usam palitos de fósforos para produzirem fogo, e graças a isso torna-se possível fazer aqueles pratos deliciosos da nossa culinária. Pensando desta forma, dá parar imaginar como seria a vida sem o fósforo.
Como se não bastasse a valiosa contribuição que o fósforo oferece para nossa sociedade, ainda sim, foi descoberto que estes preciosos palitos podem também ajudar no desenvolvimento do nosso raciocínio lógico-dedutivo. Isso através da produção de desafios de estimado valor educativo.
Estes desafios ajudam no desenvolvimento de estratégias para resolver situações problemas que nos são apresentadas, sendo utilizado de forma direta conhecimentos de matemática, tais como noções de áreas, progressões e outros mais.
Neste trabalho apresento uma seleção de alguns destes desafios que fazem uso palitos de fósforos. Tudo isso na busca de oferecer a todos um passatempo divertido e ao mesmo tempo criativo.
Não acenda o fósforo, acenda esta idéia, e mãos a obra !!!"
Wendel Melo Andrade
Apostila do jogo dos palitos
Apostila das respostas do jogo
OBS: os arquivo estão no formato do word 97-2003 quero dizer que você pode baixar facilmente no broffice e no word 2010
Caso você não tenham palito e gosta de internet veja que encontrei o jogo dos palitos online e se divirtam-se com matemática!!!
Jogos dos palitos online
Assinar:
Comentários (Atom)
O DIA NACIONAL DA MATEMÁTICA DIA 6 DE MAIO SE APROXIMA ...
O DIA NACIONAL DA MATEMÁTICA DIA 6 DE MAIO SE APROXIMA ...
Algumas Ideias e sugestões e muito mais... Sobre o Dia Nacional da Matemática A iniciativa de instituir o Dia da Mate...

-
NÃO PODERIA ESQUECER DOS MEUS COLEGAS PROFESSORES DE PORTUGUÊS! Andei vasculhando na net e olhe o que encontrei é "Soletr...
-
Eu estava vasculhando meus arquivos da época da FACU olha só que encontrei: o jogo dos palitos, logo abaixo irei postar o link d...
-
Descobri no site Escola Games o jogo educacional Algarismos Romanos para os alunos do EF I FONTE: http://www.escolagames.com.br...



























