”Para os matemáticos, um eterno problema é explicar ao grande público que a importância da Matemática vai além de sua aplicabilidade. É como explicar a alguém que nunca ouviu música e beleza de uma melodia… Que se aprenda a Matemática que se resolvem problemas práticos da vida, mas que não se pense que esta é a sua qualidade essencial. Existe uma grande tradição cultural a ser preservada e enriquecida, em cada geração." Chandier & Edwards Mathematical Intelligencer. p.35, 1998.
quarta-feira, 17 de maio de 2017
terça-feira, 25 de abril de 2017
PLATAFORMA YOUTUBE EDUCAÇÃO
YouTube/Edu, é um canal dedicado a vídeos
educacionais desenvolvido em parceria com a Fundação Lemann e o Google, para a criação de
uma página exclusiva do YouTube, na qual professores, gestores e alunos podem
encontrar conteúdos educacionais gratuitos e de qualidade, em Português.
Fonte: https://www.youtube.com/channel/UCs_n045yHUiC-CR2s8AjIwg,
visitado em 09/04/2015
Poderá também gostar de:
domingo, 2 de abril de 2017
O DIA NACIONAL DA MATEMÁTICA DIA 6 DE MAIO SE APROXIMA ...
Algumas Ideias e sugestões e muito
mais...
Sobre o Dia
Nacional da Matemática
A iniciativa de instituir o Dia da
Matemática no dia 6 de maio, partiu da comissão organizadora do Centenário de
Malba Tahan em1995, formada por Pedro Paulo Salles (educador musical e sobrinho
neto), André Pereira (historiador e neto), prof. Bigode, Valdemar Vello (editor
e especialista em Malba Tahan) e Atílio Bari (teatrólogo) todos de certo modo especialistas
em Malba Tahan cada um na sua especialidade. A proposta do dia da matemática
foi apresentada e entusiasticamente abraçada pelo saudoso educador Darcy
Ribeiro que na época era senador pelo estado do Rio de Janeiro.
Dentre os vários eventos
organizados por conta do centenário, destaque-se a apresentação da peça “O
Homem que Calculava” encenada pela companhia Teatral dirigida por Atílio Bari,
no prédio da Bienal do Ibirapuera em São Paulo; palestras, artigos, etc. A
propósito a peça teatral foi apresentada para centenas de milhares de alunos
durante mais de 10 anos.
O dia da Matemática foi aprovado
no ano de 1995 pela Assembleia Legislativa do Rio de Janeiro e pela Câmara
Municipal de São Paulo, mais tarde a direção da SBEM deu continuidade à
campanha do dia da matemática apresentando o projeto do velho Darcy, que acabou
sendo aprovado na Câmara Federal através de uma deputada do estado de Goiás.
Recentemente a Assembleia Legislativa da Bahia também instituiu a data, que tem
entre seus objetivos mobilizar alunos e professores para desenvolver projetos,
explorar e promover a matemática em suas várias dimensões entre elas a
recreativa, a cultura, a utilitária e outras que lhe dão significado.
Centenas de escolas tem programado
a Semana da Matemática nos dias próximos de 6 de maio, feiras de matemática
(bastante populares em Santa Catarina), exposições de trabalhos de alunos, em
especial com temas geométricos e suas conexões com as artes, a arquitetura, etc.;
encenações de peças teatrais; apresentações em Power point e animações de projetos
desenvolvidos por alunos; apresentações de trabalhos de pesquisa sobre episódios
da História da Matemática; gincanas e olimpíadas de Matemática Recreativa com
desafios, quebra-cabeças, jogos lógicos; exposições de arte e de fotografias
matemáticas que mostram a presença da matemática no cotidiano e nas outras áreas
do conhecimento; recitais de poesia, música, etc.
O dia da matemática é comemorado em
várias partes do mundo, na Espanha como no Brasil o dia é comemorado na data de
nascimento de um matemático (lá é dia da matemática é 12 de maio, data de nascimento
de Puig Adam, o mais importante educador matemático espanhol), em outros países
como nos EUA no dia 14 de março, “O dia do Pi”, pois lá a data se escreve
3,14;em alguns lugares a data é comemorada no dia 22 de julho em alusão a
22/7que é uma aproximação de Pi descoberta por Arquimedes de Siracusa.
Dia Nacional da
Matemática – 6 de Maio
Aqui
algumas sugestões de atividades para serem realizadas, no dia 06 de maio, em
comemoração ao Dia Nacional da Matemática.
Exibição de Filme, Vídeo
ou Execução de um Áudio: http://www.matematica.seed.pr.gov.br/modules/conteudo/conteudo.php?conteudo=206
História em quadrinhos: http://www.matematica.seed.pr.gov.br/modules/conteudo/conteudo.php?conteudo=208
Oficina de jogos
matemáticos: http://www.matematica.seed.pr.gov.br/modules/conteudo/conteudo.php?conteudo=213
Matemática e Literatura: http://www.matematica.seed.pr.gov.br/modules/conteudo/conteudo.php?conteudo=214
Matemática e Música: http://www.matematica.seed.pr.gov.br/modules/conteudo/conteudo.php?conteudo=215
Resolução de Problemas: http://www.http://www.matematica.seed.pr.gov.br/modules/conteudo/conteudo.php?conteudo=207
Dia 14 de março (3,14…)
DIA INTERNACIONAL DE PI – http://www.piday.org/
Dia 7 de março (Dia
MUNDIAL de Matemática) http://www.worldmathsday.com/
Outros dias da Matemática
organizados por instituições: http://www.msri.org/people/members/chillar/badmathday/
terça-feira, 7 de fevereiro de 2017
POESIA MATEMÁTICA
Millôr Fernandes
Às folhas tantas
do livro matemático
um Quociente apaixonou-se
um dia
doidamente
por uma Incógnita.
Olhou-a com seu olhar inumerável
e viu-a do ápice à base
uma figura ímpar;
olhos rombóides, boca trapezóide,
corpo retangular, seios esferóides.

Fez de sua uma vida
paralela à dela
até que se encontraram
no infinito.
"Quem és tu?", indagou ele
em ânsia radical.
"Sou a soma do quadrado dos catetos.
Mas pode me chamar de Hipotenusa."
E de falarem descobriram que eram
(o que em aritmética corresponde
a almas irmãs)
primos entre si.
E assim se amaram
ao quadrado da velocidade da luz
numa sexta potenciação
traçando
ao sabor do momento
e da paixão
retas, curvas, círculos e linhas sinoidais
nos jardins da quarta dimensão.
E enfim resolveram se casar
constituir um lar,
mais que um lar,
um perpendicular.

Convidaram para padrinhos
o Poliedro e a Bissetriz.
E fizeram planos, equações e diagramas para o futuro
sonhando com uma felicidade
integral e diferencial.
E se casaram e tiveram uma secante e três cones
muito engraçadinhos.
Foi então que surgiuE foram felizes
até aquele dia
em que tudo vira afinal
monotonia.
Era o triângulo,Ofereceu-lhe, a ela,
uma grandeza absoluta
e reduziu-a a um denominador comum.
Ele, Quociente, percebeu
que com ela não formava mais um todo,
uma unidade.
tanto chamado amoroso.
Desse problema ela era uma fração,

Mas foi então que Einstein descobriu a Relatividade
e tudo que era espúrio passou a ser
moralidade
como aliás em qualquer
sociedade.
Texto extraído do livro "Tempo e Contratempo", Edições O Cruzeiro - Rio de Janeiro, 1954, pág. sem número, publicado com o pseudônimo de Vão Gogo.
Sugestão de Trabalho
I- Ler com a turma a poesia, fazer levantamento das palavras/ termos matemáticos apresentados observando o sentido dentro da mesma.
II- Relacionar as palavras abaixo com sua definição:
a)Poliedro
b)Bissetyriz
c)Rombóide
d)Trapezóide
e)Linhas senoidais
f)Cone
g)Círculos concêntricos
h)Secante
- Quadrilátero de ângulos não-retos, de lados opostos iguais e lados contíguos diferentes.
- Diz-se dalinha ou superfície que corta outra.
- Semirreta que parte do vértice de um ângulo e forma com seu lados ângulos adjacentes e iguais.
- Círculos que tem o mesmo centro.
- Sólido limitado lateralmente por um superfície cônica.
- Sólido limitado por superfícies planas.
- Quadrilátero que só tem dois laods paralelos.
- Movimentos de caracter´ssticas sinuosas e periódicas.
IV - Pesquisa o significado de cada conceito grifado e represente simbolicamente.
V - Em grupos confeccionar um cartaz ilustrando o tema da poesia
VI _ Leia:
"...indagou ele /Com ânsia radical."
Qual o significado das palavras em destaque?
VII - Observe a seguinte frase:
"Escandalizaram os ortodoxos das fórmulas euclidianas."
Ortodoxos significa:
a) pessoas corretas;
b) as pessoas que seguem uma doutrina estabelecida;
c) as pessoas velhas.
VIII - É também oportuno para início do trabalho de geometria, pois muitos conceitos da mesma são tratados na poesia.
Bom Trabalho.
Profª Senhorinha da Silva Goi
segunda-feira, 22 de agosto de 2016
TABUADA, MEDIDAS E OPERAÇÕES
6 º ano
NÚMEROS E OPERAÇÕES, GRANDEZAS E MEDIDAS
Conteúdo: multiplicações, medidas de superfície, unidades de área, formas geométricas, quadrados perfeitos ou números quadrados, potências e ângulos.
JUSTIFICATIVA
Encaminhar para o aluno resolver problemas do seu
cotidiano relacionados à unidades de medidas, partindo de situações simples.
Objetivos:
- Construir os conceitos básicos da tabuada de multiplicar e suas regularidades e padrões entre si;
- Relacionar tabuada com medidas de área, sejam capazes de construir diferentes figuras com mesma áreas;
- Reconhecer as diferentes formas de calcular a área de quadrados e retângulos;
- Utilizar as unidades padrões de superfícies, bem como seus múltiplos e submúltiplos;
- Analisar múltiplos e divisores de números naturais;
- Deduzir as fórmulas de cálculo de aérea e perímetro de figuras geométricas;
- Deduzir maneiras de como calcular de área s através de enquadramentos e decomposição de figuras.
ATIVIDADE I: Construindo a tabuada na forma de quadrados:
Materiais: 1 folha A3 com quadriculada de 1cm2, por grupo,
lápis de cor e régua.
1: Traçado dos quadrados em diagonal
1.1. Desenhar na folha quadriculada um quadrado de lado
um, começando num ponto qualquer na zona superior esquerda da folha e deixando
uma pequena margem.
1.2. Unindo o vértice inferior direito do
primeiro quadrado com o vértice superior esquerdo do segundo quadrado e assim
sucessivamente, desenhar quadrados de lados 2, 3, 4, 5 e 6.
1.3. Pintar o interior de todos os quadrados, usando
sempre a mesma cor.
2: Traçando retângulos:

2.1 . Traçar retas prolongando-se os lados dos quadrados já desenhados.
2.2.Pintar, da mesma cor, as figuras geometricamente iguais resultantes do traçado feito.
 2.3. No interior de cada figura desenhada, registar o valor da respectiva área, sob a forma
2.3. No interior de cada figura desenhada, registar o valor da respectiva área, sob a forma
de uma multiplicação, em que os fatores são o número de linhas e o número de
quadrículas por linha. Ex.: A área de um retângulo com 6 quadradinho pode resultar de
1x6 ou 2x3, consoante(ao lado do outro) o retângulo ocupe 1 linha com 6 quadrículas, ou 2 linhas com 3 quadradinho de cada uma.
3: Continue o traçando:
A construção que acabou de fazer pode ser continuada. Continue-a, seguindo os
procedimentos anteriores, até que a folha de papel o permita.
Parte II: Procurando regularidades na tabuada e nas formas.
Observe a construção feita. Descubra e registe regularidades.
Parte III: Explorando a tabuada e suas formas
Questões orientadoras
1. Procurar todas as figuras de área 12. Quantas figuras se encontram? Identificar as figuras geometricamente iguais. Quantos grupos diferentes se encontram? Que representam s diferentes factores de 12?
2. Indicar se é verdadeira ou falsa a afirmação: “Duas figuras geometricamente iguais são equivalentes, mas duas figuras equivalentes podem não ser geometricamente iguais”. Justificar a resposta.
3. Dar exemplos de figuras equivalentes mas que não sejam geometricamente iguais. Localizar todas as figuras de perímetro 20. Qual destas figuras tem maior área? Acontecerá o mesmo para outras figuras isoparamétricas(figuras de perímetros iguais)? m que regularidades se encontram?
4. Localizar os múltiplos de 2, de 3, de 4, de 5, de 6, .... Onde estão, na tabuada e suas formas os múltiplos comuns a 2 e a 4? Porquê? E os múltiplos comuns a 2 e a 3? Porquê?
5. Procurar todas as figuras de área 12 e de área 15. Usar as decomposições do 12 e do 15 em fatores para calcular 12 x 15. Alguma(s) combinação de fatores tornou o cálculo mais simples? Qual/Quais? Porquê?
6. Calcular agora a área do retângulo representada por 12 x 15 de uma outra forma. Haverá alguma forma de representar a área deste retângulo através de retângulos representados na tabuada? Se sim, que retângulos são estes?
7. A sala da Joana tem de área 25 m2 e suas formas” para descobrir que diferentes formas geométricas pode ter a sala da Maria. Desenhar um esquema da sala em papel quadriculado.
8. Na “tabuada geométrica” há figuras cuja área se pode representar sob a forma de, um
produto de dois fatores iguais. Que figuras são? Como descrever a sua localização?
Representar a sua área sob a forma de potência.
9. O que representam geometricamente as potências de expoente 2? Qual é o número quadrado que vem a seguir ao 64? E a seguir? E a seguir?...
O numero 40 é um quadrado perfeito? Porquê?
Escolher duas figuras geometricamente iguais e localizá-las na “tabuada geométrica”. As áreas destas figuras podem representar-se sob a forma de potência de expoente 2?
10. Os quadrados são retângulos porque têm os ângulos retos.
Indicar se é verdadeira ou falsa a afirmação: “Os quadrados são retângulos mas nem todos os retângulos são quadrados”. Justificar a resposta.
11. Há números na “tabuada geométrica” a que só pode associar-se um par de figuras geometricamente iguais. Que números são esses?
Fonte:
Escola Superior de Educação do Instituto Politécnico de Setúbal Programa de Formação Contínua em Matemática para Professores dos 1.º e 2.º Ciclos do Ensino Básico: 2010 ‐ 2011
. PARTE IV - ATIVIDADES GERAIS
PERÍMETRO DE UM POLÍGONO

O perímetro de uma figura plana fechada é o comprimento da linha que limita a figura.
É o comprimento da linha que limita o polígono ou a soma das medidas dos seus lados.

.
Perímetro=100+50+97+10+13+10+10+30= 320m
PERÍMETRO DE UM POLÍGONO:
Retângulo

Quadrado
P = l + l + l+ l
Perímetro = 4 x l
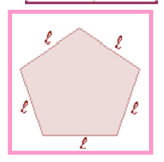
Pentágono
P= l + l + l + l + l
Perímetro= 5 x l
DETERMINAÇÃO NA PRÁTICA
Diâmetro – Corda que passa pelo centro da circunferência.(AC)
 Diâmetro (d)=2xraio(r)
Diâmetro (d)=2xraio(r)
Raio – Metade do diâmetro.(AO , OC, OB)
Círculo é uma figura geométrica plana constituída por uma circunferência e pelo conjunto de pontos do seu espaço interior
DETERMINAÇÃO PRÁTICA DO π
O quociente do comprimento de uma circunferência pelo seu diâmetro tem sempre o mesmo valor que se designa por π (PI). O seu valor, aproximado às centésimas, é de 3,14.
PERÍMETRO DO CÍRCULO OU COMPRIMENTO DA CIRCUNFERÊNCIA
 Perímetro de um círculo é o comprimento da circunferência que o limita.
Perímetro de um círculo é o comprimento da circunferência que o limita.
Para calcularmos o perímetro do círculo multiplicamos π pelo comprimento do diâmetro.
P = π X d
Como diâmetro = 2x raio podemos também dizer que:
PERÍMETRO DO CÍRCULO (comprimento da circunferência) = 2 x π x raio
MEDIDAS DE COMPRIMENTO (METRO)
A unidade fundamental de medidas de comprimento é o metro, indicado por m.
FIGURAS EQUIVALENTES

Duas figuras são congruentes se sobrepuserem ponto por ponto.
Figuras equivalentes são aquelas que têm a mesma área.
 Figuras planas congruentes são sempre equivalentes.
Figuras planas congruentes são sempre equivalentes.
Figuras planas equivalentes têm sempre a mesma área, mas podem ser, ou não, congruentes.
Figuras geometricamente iguais
ÁREAS EQUIVALENTES
Duas superfícies são equivalentes quando têm a mesma área, como por exemplo, as superfícies A e B.
A medida de área de uma superfície é igual ao número de vezes que a unidade de área escolhida cabe na superfície considerada.
UNIDADE DE ÁREA DO SISTEMA MÉTRICO
 Esta figura é formada por quatro quadrados.
Esta figura é formada por quatro quadrados.
Como a área de cada quadrado é 1 , a área
desta figura é 4 ,

2.1 . Traçar retas prolongando-se os lados dos quadrados já desenhados.
2.2.Pintar, da mesma cor, as figuras geometricamente iguais resultantes do traçado feito.
 2.3. No interior de cada figura desenhada, registar o valor da respectiva área, sob a forma
2.3. No interior de cada figura desenhada, registar o valor da respectiva área, sob a formade uma multiplicação, em que os fatores são o número de linhas e o número de
quadrículas por linha. Ex.: A área de um retângulo com 6 quadradinho pode resultar de
1x6 ou 2x3, consoante(ao lado do outro) o retângulo ocupe 1 linha com 6 quadrículas, ou 2 linhas com 3 quadradinho de cada uma.
A construção que acabou de fazer pode ser continuada. Continue-a, seguindo os
procedimentos anteriores, até que a folha de papel o permita.
Parte II: Procurando regularidades na tabuada e nas formas.
Observe a construção feita. Descubra e registe regularidades.
Parte III: Explorando a tabuada e suas formas
Questões orientadoras
1. Procurar todas as figuras de área 12. Quantas figuras se encontram? Identificar as figuras geometricamente iguais. Quantos grupos diferentes se encontram? Que representam s diferentes factores de 12?
2. Indicar se é verdadeira ou falsa a afirmação: “Duas figuras geometricamente iguais são equivalentes, mas duas figuras equivalentes podem não ser geometricamente iguais”. Justificar a resposta.
3. Dar exemplos de figuras equivalentes mas que não sejam geometricamente iguais. Localizar todas as figuras de perímetro 20. Qual destas figuras tem maior área? Acontecerá o mesmo para outras figuras isoparamétricas(figuras de perímetros iguais)? m que regularidades se encontram?
4. Localizar os múltiplos de 2, de 3, de 4, de 5, de 6, .... Onde estão, na tabuada e suas formas os múltiplos comuns a 2 e a 4? Porquê? E os múltiplos comuns a 2 e a 3? Porquê?
5. Procurar todas as figuras de área 12 e de área 15. Usar as decomposições do 12 e do 15 em fatores para calcular 12 x 15. Alguma(s) combinação de fatores tornou o cálculo mais simples? Qual/Quais? Porquê?
6. Calcular agora a área do retângulo representada por 12 x 15 de uma outra forma. Haverá alguma forma de representar a área deste retângulo através de retângulos representados na tabuada? Se sim, que retângulos são estes?
7. A sala da Joana tem de área 25 m2 e suas formas” para descobrir que diferentes formas geométricas pode ter a sala da Maria. Desenhar um esquema da sala em papel quadriculado.
8. Na “tabuada geométrica” há figuras cuja área se pode representar sob a forma de, um
produto de dois fatores iguais. Que figuras são? Como descrever a sua localização?
Representar a sua área sob a forma de potência.
9. O que representam geometricamente as potências de expoente 2? Qual é o número quadrado que vem a seguir ao 64? E a seguir? E a seguir?...
O numero 40 é um quadrado perfeito? Porquê?
Escolher duas figuras geometricamente iguais e localizá-las na “tabuada geométrica”. As áreas destas figuras podem representar-se sob a forma de potência de expoente 2?
10. Os quadrados são retângulos porque têm os ângulos retos.
Indicar se é verdadeira ou falsa a afirmação: “Os quadrados são retângulos mas nem todos os retângulos são quadrados”. Justificar a resposta.
11. Há números na “tabuada geométrica” a que só pode associar-se um par de figuras geometricamente iguais. Que números são esses?
Fonte:
Escola Superior de Educação do Instituto Politécnico de Setúbal Programa de Formação Contínua em Matemática para Professores dos 1.º e 2.º Ciclos do Ensino Básico: 2010 ‐ 2011
. PARTE IV - ATIVIDADES GERAIS
PERÍMETRO DE UM POLÍGONO

O perímetro de uma figura plana fechada é o comprimento da linha que limita a figura.
É o comprimento da linha que limita o polígono ou a soma das medidas dos seus lados.

.
Perímetro=100+50+97+10+13+10+10+30= 320m
PERÍMETRO DE UM POLÍGONO:
Exemplos
b - base ou comprimento
h - altura ou largura
Perímetro = 2b + 2h,onde b= base h=altura

Quadrado
P = l + l + l+ l
Perímetro = 4 x l

Pentágono
P= l + l + l + l + l
Perímetro= 5 x l
V - ELEMENTOS DE UMA CIRCUNFERÊNCIA
Diâmetro – Corda que passa pelo centro da circunferência.(AC)
 Diâmetro (d)=2xraio(r)
Diâmetro (d)=2xraio(r)Raio – Metade do diâmetro.(AO , OC, OB)
Círculo é uma figura geométrica plana constituída por uma circunferência e pelo conjunto de pontos do seu espaço interior
DETERMINAÇÃO PRÁTICA DO π
O quociente do comprimento de uma circunferência pelo seu diâmetro tem sempre o mesmo valor que se designa por π (PI). O seu valor, aproximado às centésimas, é de 3,14.
PERÍMETRO DO CÍRCULO OU COMPRIMENTO DA CIRCUNFERÊNCIA
 Perímetro de um círculo é o comprimento da circunferência que o limita.
Perímetro de um círculo é o comprimento da circunferência que o limita.Para calcularmos o perímetro do círculo multiplicamos π pelo comprimento do diâmetro.
P = π X d
Como diâmetro = 2x raio podemos também dizer que:
PERÍMETRO DO CÍRCULO (comprimento da circunferência) = 2 x π x raio
MEDIDAS DE COMPRIMENTO (METRO)
A unidade fundamental de medidas de comprimento é o metro, indicado por m.
FIGURAS EQUIVALENTES

Duas figuras são congruentes se sobrepuserem ponto por ponto.
Figuras equivalentes são aquelas que têm a mesma área.
 Figuras planas congruentes são sempre equivalentes.
Figuras planas congruentes são sempre equivalentes.Figuras planas equivalentes têm sempre a mesma área, mas podem ser, ou não, congruentes.
Figuras geometricamente iguais
ÁREAS EQUIVALENTES
Duas superfícies são equivalentes quando têm a mesma área, como por exemplo, as superfícies A e B.
A medida de área de uma superfície é igual ao número de vezes que a unidade de área escolhida cabe na superfície considerada.
A medida da área depende dependa da unida escolhida.
UNIDADE DE ÁREA DO SISTEMA MÉTRICO
O metro quadrado representa a área de um quadrado de 1 metro de lado e é a unidade de área do sistema métrico.
RECORDA
 Esta figura é formada por quatro quadrados.
Esta figura é formada por quatro quadrados.Como a área de cada quadrado é 1 , a área
desta figura é 4 ,
1 m2
= 100 dm2 5 cm2 = 0,05 dm2
ÁREA DO TRIÂNGULO
Área do triângulo= b x h
2
b = base
h = altura
ÁREA DO CÍRCULO
Área= π .r2
r2 =
r x r
r = raio
raio = diâmetro
2
ÁREA DO RETÂNGULO E DO QUADRADO
Área do retângulo = b x a
b= base ; a= altura
ÁREA DO PARALELOGRAMO
Área do paralelogramo = b x a
b= base ; a= altura
ÁREAS POR DECOMPOSIÇÃO

ÁREA POR ENQUADRAMENTO

Nem sempre é possível determinar o valor exato da medida da área de uma superfície. Nestes casos, procuramos um valor aproximado, enquadrando a superfície.
A medida da área da piscina é maior que 33 m2.
A medida da
área da piscina é menor que 53 m2.
33 m2
< área da piscina < 53 m2
Pode-se explorar de diferentes maneiras as fórmulas de cálculos de área e perímetros das figuras geométricas.
Assinar:
Comentários (Atom)
O DIA NACIONAL DA MATEMÁTICA DIA 6 DE MAIO SE APROXIMA ...
O DIA NACIONAL DA MATEMÁTICA DIA 6 DE MAIO SE APROXIMA ...
Algumas Ideias e sugestões e muito mais... Sobre o Dia Nacional da Matemática A iniciativa de instituir o Dia da Mate...

-
NÃO PODERIA ESQUECER DOS MEUS COLEGAS PROFESSORES DE PORTUGUÊS! Andei vasculhando na net e olhe o que encontrei é "Soletr...
-
Eu estava vasculhando meus arquivos da época da FACU olha só que encontrei: o jogo dos palitos, logo abaixo irei postar o link d...
-
Descobri no site Escola Games o jogo educacional Algarismos Romanos para os alunos do EF I FONTE: http://www.escolagames.com.br...


































